|
As to the determination of bearing capacity of the soil beneath a shallow footing, K. Terzaghi1) has defined two types of failure, i.e., failure by general shear and by local shear. Corresponding to these two types of failure, he also has obtained respective equations which are known as Terzaghi's bearing capacity formulas
Note that, in eq. (1) and (3), the ultimate bearing capacity in bracket is divided by a factor of safety 3 to obtain allowable bearing value.
The values of bearing-capacity factors expressed by eq. (2) and. (4)
are shown by thick curves in Fig. 1 through Fig.3 as functions of angle
of internal friction 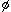 and are also given in a tabular form in Table 2.
and are also given in a tabular form in Table 2.
For the proper choice between either eq. (1) or eq. (3), Terzaghi1) and Terzaghi-Peck2) specify that eq. (1) is to be used when the soil is fairly dense or stiff and, its mechanical properties are such that the strain which precedes the failure of the soil by plastic flow is very small, and that eq. (2) corresponds to the condition that the soil is loose or fairly soft and the footing considerably settles into the ground before the state of plastic equilibrium spreads as far as the theoretically assumed boundary. P. C. Rutledge, formerly Professor at North-western University, has instructed in his classroom lecture to use
-
eq. (1) for dense sands and medium to stiff clay type soils;
eq. (3) for loose sands, soft plastic clays, and compressible soils.
However, it seems more convenient from a practical viewpoint if a single set of bearing-capacity factors may be made available which approximates the values given in eq. (4) in the range of small angles of internal friction and, with the increase of angle of internal friction, approaches to the values determined by eq.(2) so that for a given soil no difficulty is encountered in the choice between two different types of expected failure. An answer to this problem has been already furnished by Peck-Hanson-Thornburn3) in their textbook, in which a single curve for each of Nq and Nr is given as shown by dashed lines in Fig.2 and Fig.3. To the writer, however, any information for the basis, which the derivation of the curves in this textbook is based on, is not available.
|