A vector having three components X₁, X₂, X₃ in three independent references may be expressed with a row matrix (X₁ X₂ X₃) or a column matrix 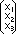. The merits of these vector notations depend upon that not only the matrix calculation is easy to apply for vectors but also the transformation from one vector field to the other is convenient to obtain with the linear transformation matrix. In this paper the column matrices of order three are mostly used as the three dimensional vector quantities and the component of which about ƒ¿- or x-axis is placed in the first row and the components of which about ƒÀ- or y-axis and ƒÁ- or z-axis are placed in the second and the third row of the column matrices respectively.

The first part of this paper shows the extension of the slope deflection equations to the spatial members in terms of matrix elements under the following conditions:

a)	The materials of the structure are assumed to be perfectly elastic.
b)	All displacements are considered small compare to the over-all dimension of the structure so that it is admissible to satisfy the equilibrium conditions in the undeformed rather than in the deformed configuration.
c)	As a consequence instability of the member is ignored for the analysis.

Then the analysis of the framework structures is discussed and the method of analysis is illustrated by means of an example.